损失函数，MLE，MAP，ERM的关系

以前的，整理到网站上x2

关系

关系：根据ERM的思想需要一个损失函数，而MLE的相反数可以作为损失函数

$L(\theta)$是极大似然估计MLE，$J(\theta)$是基于经验风险最小化ERM的损失函数Loss Function

交叉熵损失函数推导

下面给出交叉熵损失函数的推导（二分类为例，以MLE方法推导）

对于二分类问题，可以作出如下式子，使该式子最大化的参数$\theta$即为MLE方法：

$$l(\theta)=\prod_{i=1}^N[\pi(x_i)]^{y_i}[1-\pi(x_i)]^{1-y_i}$$ $$MLE：\arg\max_\theta l(\theta)$$

【【其中，$\pi(x_i)$即为预测结果（模型输出；输入$x_i$，经过模型之后输出$ \pi(x_i)$，在损失函数中为一个关于输入$x_i$的函数），$y_i$即为对应的真实标签】】

对于交叉熵损失函数来说，如果最后一层softmax生成概率，那么这个输出需处理为经过阈值后的确定标签

于是我们要让乘法的概率，即最大似然估计（下面这个式子）最大化（以下以像LR的二分类为例）

$$MLE_{P(y|x)}=\prod_{i=1}^N[\pi(x_i)]^{y_i}[1-\pi(x_i)]^{1-y_i}$$

【其中，$\pi(x_i)$即为预测标签（模型输出），$y_i$即为对应的真实标签】

【这个式子将多分类的多项之积的MLE写成一个式子，当$y_i=1$时，只有$[\pi(x_i)]^{y_i}$会生效，$[1-\pi(x_i)]^{1-y_i}$由于指数部分为0使得该子项等于1；反之$y_i=0$时，只有后半部分会生效。】

【于是当比如真实标签$y_i=1$时，左边部分生效，那么$\pi(x_i)$的输出越小，即输出概率越偏离真实值，MLE整体就越小，而我们就是要在整体样本之上极大化MLE，也就是尽量让输出概率整体接近真实值，此即MLE的意义】

取对数变成：

$$L(\theta)=\sum_{i=1}^N[y_i\log \pi(x_i)+(1-y_i)\log(1-\pi(x_i))]$$

MLR的相反数其等价于ERM方法的损失函数（$m$为mini-batch size）：

$$J(\theta)=-\frac{1}{m}L(\theta)$$

于是定义好了损失函数，根据ERM思想我们想要最小化损失函数，即求使得损失函数极小值下的参数$\theta$。但往往直接求0导得极值无法做到，因为参数众多无法求解，于是常用牛顿拟牛顿法，梯度下降法解决

以梯度下降法为例，对损失函数用参数$\theta$求偏导：$\nabla_\theta L(\theta)$，然后在各个$\theta_i$的方向上梯度下降，这里写总式：$\theta\to \theta+\nabla_\theta L(\theta)$

其中$\nabla_\theta L(\theta)$这样求: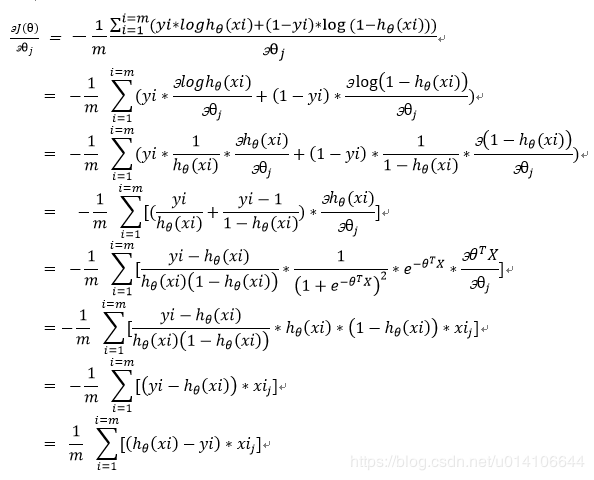

这里的$h(x_i)$即上面的$\pi(x_i)$。即输入$x_i$，经过模型之后输出

P.S. 交叉熵还可以从信息论角度推导，通过信息熵相对熵推导出交叉熵

交叉熵标准表达式

$$H(p,q)=-\sum p(x)\log q(x)$$

其中$p(x)$是真实标签，$q(x)$是模型预测

注意一个理解，这里容易混淆，多分类，比如一个手写数字识别，是个十分类任务，0~9共十个类别。

对于识别数字1，神经网络的输出结果越接近[0,1,0,0,0,0,0,0,0,0]

若模型输出为[0.2,0.8,0.34,0.2,0.6,0.7,0.7,0.7,0.6,0.2] （显然这个没有经过softmax层）

那么反应在交叉熵损失函数上，则为：$H(·)=-(0×\log0.2+1×\log0.8+0×\log0.34+0×\cdots)$

只有在正确分类上才生效，其它的都不生效

正确的理解这个形式

多层神经网络（MLP）用SGD求损失函数最小化

深度神经网络使用交叉熵损失函数也是同理：可以想象对于神经网络来说，其用梯度下降法求导是非常复杂的，因为多层神经网络模型输出的预测函数$h(x_i)$非常复杂，其有非常多的中间变量（隐藏层结点），于是在使用梯度下降法，对$J(\theta)$求导的时候，其中的子项$\frac{\partial h(x_i)}{\partial x_i}$是个非常庞大的过程，需要根据链式法则逐渐传导回输入层$x_i$，于是就发明了反向传播（BP）算法来便于计算，见以前的文章对BP的理解。

无论是交叉熵还是MSE还是其它损失函数，使用SGD都要涉及对MLP模型的预测输出$\hat y=h(x_i)$求对输入$x_i$的偏导

Q：交叉熵适合分类问题，MSE适合回归问题

回归问题指输入可以是连续的（实数）或无上下界

1. 分类问题使用交叉熵：

   ①均方误差损失函数一般是非凸函数（non-convex），其在使用梯度下降算法的时候，容易得到局部最优解，而不是全局最优解。因此要选择凸函数（二阶导大于等于0）。不过在LR中，交叉熵是凸函数，所以LR中必用交叉熵。而在多层神经网络（MLP）中，交叉熵是非凸函数了。
   ②使用MSE的另一个缺点就是其偏导值在输出概率值接近0或者接近1的时候非常小，这可能会造成模型刚开始训练时，偏导值几乎消失。

   当然了，分类问题也是可以使用MSE的，不过因为以上原因效果不好

2. 回归问题使用MSE：

   交叉熵的损失函数【只和分类正确】的预测结果有关系（根据前面的推导式子，显然对于分类错误的项，不会生效，直接变为常数项（乘1）），而MSE的损失函数不仅和分类正确的预测结果有关，【还和错误的分类有关系】，所以回归问题不能用交叉熵！

   见上面“交叉熵标准表达式”的例子

MAP

贝叶斯学派，最大后验估计

略